
கணிதத்தில் பொன் விகிதம் (Golden Ratio) மற்றும் ஃபிபனாச்சி எண்கள் (Fibonacci Numbers) என்றால் என்ன?
கணிதத்தில் பொன்விகிதம் (Golden Ratio – phi – φ) என்பது ஒரு அழகிய மந்திர எண்ணைப் போன்றது. நாம் பார்க்கும் பெரும்பாலான இடங்கள் மற்றும் பொருட்களில் எல்லாம் இந்த எண் பொதிந்து இருப்பதைக் காணலாம். இதன் சிறப்புகளைப் பற்றியும், விளக்கங்களைப் பற்றியும் இந்தப் பகுதியில் பார்ப்போம்! மேலும் பொன்விகித்தை உள்ளடக்கிய ஃபிபனாச்சி எண் தொடரின் சிறப்புகள் பற்றியும் பார்ப்போம்!
பொன் விகிதத்தின் (ஃபை – Golden Ratio – phi – φ) மதிப்பு ஏறத்தாழ 1.618 ஆகும்.
உலகப்புகழ்பெற்ற வடிவங்களில் பொன்விகிதம் (Golden Ratio – Phi – φ)
நம் முக வடிவத்தின் ரகசியம் இந்த பொன்விகிதத்தில் பொதிந்துள்ளது! பொன் விகித்திற்கு ஏற்ப ஒருவரது முகவடிவம் அமைந்து இருந்தால் (அதாவது, a/b = 1.618; இதில் a மற்றும் b மேலேயுள்ள படத்தில் காட்டப்பட்டுள்ளது.), அவர் மிகவும் அழகானவராக இருப்பாராம்! பொன்விகித்தில் அமைந்த உருவங்களும், கட்டடங்களும், படங்களும், மிக அழகான வடிவங்களைப் பெறுகின்றன.
பண்டைய கிரேக்கக் கட்டடக்கலையிலும் பொன்விகிதத்திற்கு ஏற்றவாறு கட்டடங்கள் அமைந்துள்ளதாகக் கூறப்படுகிறது. கிசாவில் அமைந்துள்ள பிரமிடுகளின் அடித்தள அகலத்துக்கும் (756 அடி) உயரத்துக்கும் (481 அடி) உள்ள விகிதம் ஏறத்தாழ 1.6 ஆக உள்ளது.

கிரேக்கக் கட்டடக்கலை 
பிரமிடு 
மோனாலிசா
உலகப்புகழ்பெற்ற லியானார்டோ டா வின்சியின் ஓவியங்களும் பொன்விகித்தில் அமைந்துள்ளதாம். மனிதன் உருவாக்கிய பொருட்கள் அல்லாது, இயற்கையிலும் இந்த பொன்விகிதம் பல இடங்களில் காணப்படுகிறதாம்! நம் தலையிலிருந்து வயிற்றுக்கு உள்ள உயரத்திற்கும், வயிற்றிலிருந்து கால் வரை உள்ள உயரத்திற்கும் உள்ள விகிதம் (ஏறத்தாழ 1.6) பொன்விகிதத்தை (Golden Ratio – Phi) ஒத்து உள்ளதாம். மேலும், நம் தோள்பட்டையிலிருந்து முழங்கை வரை உள்ள நீளத்திற்கும், முழங்கையிலிருந்து கைவிரல்நுனி வரையுள்ள நீளத்திற்கும் உள்ள விகிதம் கூட பொன்விகிதம் தான். அதுமட்டுமல்ல, நம் விரல்கள் கூட இந்த விகிதத்தில் தான் அமைந்துள்ளன!
பொன்விகிதத்திற்கான (Golden Ratio) விளக்கம்
ஏதேனும் இரண்டு இயல் எண்களுக்குள் (Natural Numbers) உள்ள விகிதம், அவ்விரண்டு எண்களின் கூடுதலுக்கும் அவற்றுள் பெரிய எண்ணுக்கும் உள்ள விகிதத்துக்குச் சமமாக இருந்தால் அந்த விகிதம் பொன் விகிதம் (Golden Ratio) என அழைக்கப்படும். இது φ (phi, அதாவது, ஃபை) என்ற குறியீட்டால் குறிக்கப்படுகிறது. இந்த விகிதம் φ -ன் மதிப்பு எப்போதும் ஏறத்தாழ 1.6180339… என்ற விகிதமுறா எண்ணாக (Irrational Number) இருக்கும். விகிதமுறா எண் என்பது முடிவிலா தசம எண்களைக் கொண்டு இருக்கும்.
a மற்றும் b என்ற ஏதேனும் இரு இயல் எண்களை எடுத்துக்கொண்டால், a, b-ஐ விட பெரிய எண்ணாக இருப்பின்,
φ = a/b = (a + b)/a = 1.6180339887498948 … (இதில், a > b )
இதை ஒரு கோட்டு வரைபடத்தில் பின்வருமாறு பார்க்கலாம்:

மேலுள்ள படத்தில் ஒரு கோடு இரண்டு பாகங்களாகப் பிரிக்கப்பட்டுள்ளன. அதாவது நீல நிற நீண்ட துண்டு a என்றும், பச்சை நிற குட்டையான துண்டு b என்றும் பிரிக்கப்பட்டுள்ளன. நீண்ட துண்டுக்கும் (
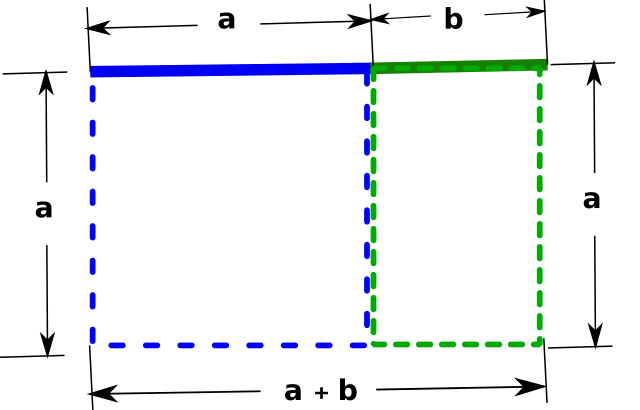
மேலேயுள்ள படம் – 1 -ல் உள்ள நேர்க்கோட்டுத் துண்டுகள் a மற்றும் b ஆகியவற்றை, சதுரம் மற்றும் செவ்வக வடிவங்கள் தோன்றுமாறு, கீழ்க்கண்டவாறு நீட்டித்தாலும் பொன்விகிதம் அமைவதைக் காணலாம்; அதாவது, நீல நிற சதுரத்தின் பக்கம் a-க்கும், பச்சை நிற செவ்வகத்தின் அகலம் b-க்கும் உள்ள விகிதம் (a/b), இந்த இரண்டு வடிவங்களையும் (நீல நிற சதுரம் மற்றும் பச்சை நிற செவ்வகம்) உள்ளடக்கிய பெரிய செவ்வகத்தின் நீளம் (a+b)-க்கும், சதுரத்தின் பக்கம் a-க்கும் உள்ள விகிதம் (a+b)/a -க்குச் சமமாக, அதாவது 1.61803… ஆக இருக்கும்.
ஃபிபனாச்சி எண் தொடர் (Fibonacci Number Sequence)
இந்த பொன் விகிதத்திற்கும் புகழ்பெற்ற ஃபிபனாச்சி எண் தொடருக்கும் (Fibonacci Number Sequence) நெருங்கிய தொடர்பு உள்ளது.
சரி! ஃபிபனாச்சி எண் தொடர் என்றால் என்ன? ஃபிபனாச்சி எண் தொடர் என்பது, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377… என்று தொடரும் எண் வரிசை. இதில், முதல் இரண்டு எண்களான 0 மற்றும் 1 தவிர, மற்ற எண்கள் அனைத்தும் ஒரே விதமான முறையைப் (Pattern) பின் தொடரும். அதாவது, முந்தைய இரண்டு எண்களின் கூடுதல் அடுத்து மூன்றாவது வரும் எண்ணாக இருக்கும். அதாவது,
- 0 + 1 = 1
- 1 + 1 = 2
- 1 + 2 = 3
- 2 + 3 = 5
- 3 + 5 = 8
- 5 + 8 = 13
- 8 + 13 = 21
- 13 + 21 = 34
- 21 + 34 = 55 …
இப்போது, ஃபிபனாச்சி எண் தொடருக்கும் பொன்விகிதத்திற்கும் என்ன தொடர்பு என்பதைப் பார்ப்போம்.
ஃபிபனாச்சி எண் தொடரில் (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, …) உள்ள இரண்டு அடுத்தடுத்த எண்களின் விகிதம், ஏறத்தாழ பொன் விகிதம் φ-க்குச் (Golden Ratio – Phi) சமமாக இருக்கும். அதாவது, இந்த எண் தொடரில், 5-க்கும் 3-க்கும் உள்ள விகிதம் 1.666. எண் 55-க்கும் 34-க்கும் உள்ள விகிதம், 1.617. எண் 233-க்கும் எண் 144-க்கும் உள்ள விதம் (233/144), 1.618055… இப்படியே, இந்தத் தொடரின் பெரிய எண்களின் விகிதங்களைக் கணக்கிட்டால், பொன் விகிதம் φ-க்குச் (Golden Ratio – Phi) சமமான எண் வருவதைப் பார்க்கலாம்.
ஃபிபனாச்சி எண் தொடரைக் கீழ்க்கண்டவாறு, படமாகப் பார்க்கலாம்:
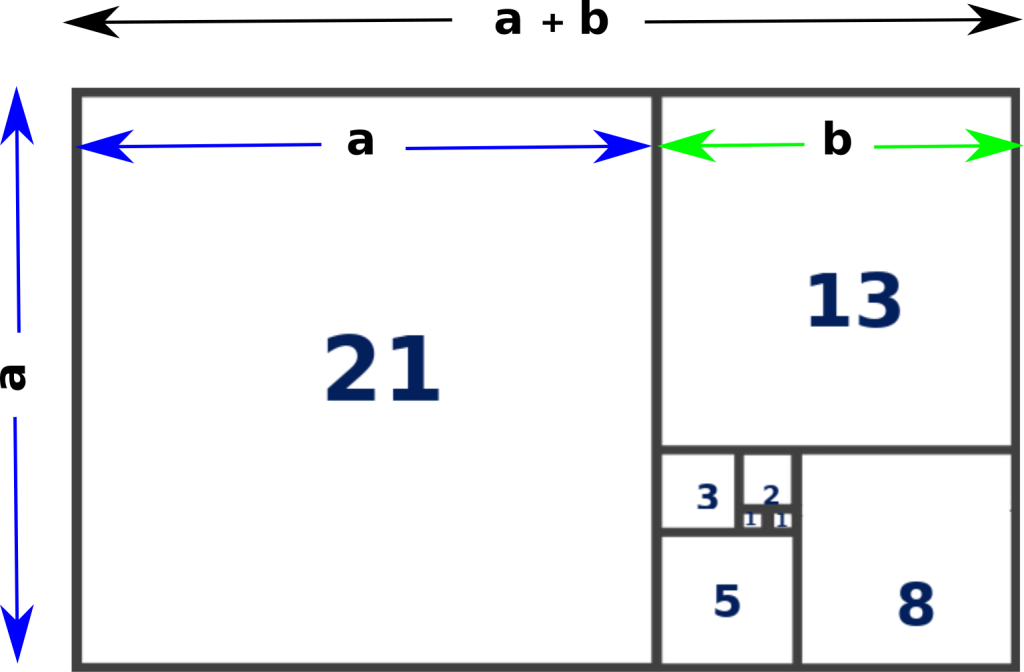
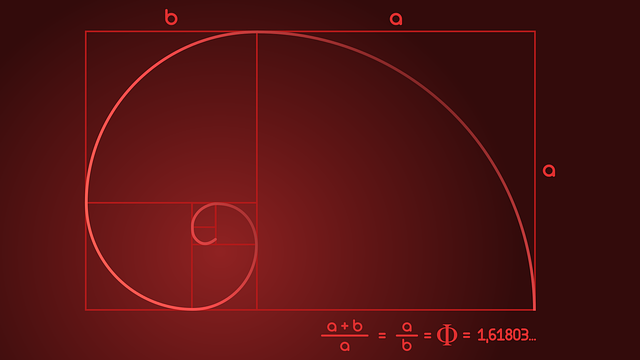
படம்-2-ல் உள்ள பொன் விகிதத்திற்கான வடிவத்தைப்போல், ஃபிபனாச்சி எண் தொடருக்கும் படம்-3-ல் உள்ளது போல் பொன் விகிதத்திற்குட்பட்ட வடிவங்களை வரைந்து கொண்டே போகலாம். படம் – 3-ல் உள்ள ஒவ்வொரு சதுரத்தின் பக்கம் (a)-வையும் ஆரமாகக் கொண்டு (Radius) வட்டத்துண்டுகள் வரைந்து கொண்டே சென்றால் கீழேயுள்ள படம்-4-ல் உள்ளதுபோல் சுருள் வடிவம் (Spiral) கிடைக்கும்.
இயற்கையின் வடிவங்களில் பொன்விகிதமும் ஃபிபனாச்சி எண் தொடரும்
இயற்கையில், இதுபோன்ற சுருள் வடிவத்தில் அமைந்தவற்றை பல இடங்களில் நாம் காணலாம். ஆம்! சங்கு, நத்தையின் ஓடு, சூரியகாந்திப்பூவின் விதைகளின் அமைப்பு, பூக்களின் வடிவம், புயல் சுழற்சியின் வடிவம், விண்வெளித்திரள் (Galaxy), இப்படி எங்கும் எதிலும் பொன்விகித்தில் அமைந்த ஃபிபனாச்சி எண் தொடரை ஒத்த சுருள் வடிவத்தைக் காணலாம்.
இப்படி எங்கும் எதிலும் பொன்விகிதம் (ஃபை – Golden Ratio – Phi) மற்றும், அந்த விகித்ததை உள்ளடக்கிய ஃபிபனாச்சி எண் தொடர் (Fibonacci Number Sequence) காணப்படுகின்றன.









Be the first to comment